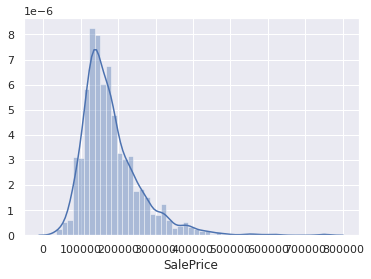
如上图所示,可以看到与使用matplotlib作的直方图最大的区别在于有一条密度曲线(KDE),可以通过设置参数去掉这条默认的曲线。另外,由上图可以知道房价呈现正态分布,还可以看到两个统计学中的概念:峰度(Kurtosis)和偏度(Skewness)。
峰度:峰度(Kurtosis)是描述某变量所有取值分布形态陡缓程度的统计量。
- Kurtosis = 0 与正态分布的陡缓程度相同
- Kurtosis > 0 比正态分布的高峰更加陡峭 —— 尖顶峰
- Kurtosis < 0 比正态分布的高峰来得平坦 —— 平顶峰
计算公式:β = M_4 / σ^4
它是和正态分布相比较的。
偏度:偏度(Skewness)是描述某变量取值分布对称性的统计量。
- Skewness = 0 分布形态与正态分布偏度相同
- Skewness > 0 正偏差数值较大,为正偏或右偏。长尾巴拖在右边。
- Skewness < 0 负偏差数值较大,为负偏或左偏。长尾巴拖在左边。
计算公式:S = (X^ - M_0) / δ
Skewness越大,分布形态偏移程度越大。
BASE ON Kaggle
Getting Started Prediction Competition
House Prices: Advanced Regression Techniques
Thx: marsggbo
版权属于:。。。源
本文链接:http://www.findmyfun.cn/kurtosis-and-skewness.html
转载时须注明出处及本声明。
我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:
https://cloud.tencent.com/developer/support-plan?invite_code=2py75w7904qok